Фонтанный код

Sep 6, 2020 · Comments
Программирование

Недавно совершенно случайно узнал про фонтанный код и поразился насколько элегантно работает этот алгоритм. Этот код позволяет надежно передавать данные по каналу с потерями без обратной связи и с минимальными накладными расходами. Более того передатчик и приемник не обязаны синхронизировать начало и конец передачи данных. Фонтанный код позволяет передатчику генерировать бесконечный поток пакетов, кодирующих исходное сообщение, а приемник может начать слушать в любой момент. Все что требуется - это принять минимально необходимое для декодирования количество пакетов. Raptor code, - одна из наиболее практичных реализаций, требует всего лишь передать всего 0.2% дополнительных пакетов для успешного декодирования с вероятностью 0.999999. При этом вероятность успешного декодирования стремительно приближается к единице с каждым дополнительным пакетом.

Зачем это нужно когда уже есть протоколы надежной передачи по двухстороннему каналу, скажем тот же TCP/IP? Оказывается существует ситуации, когда организация обратного канала связи требует изобретения машины времени. Когда нам нужно восстановить данные со сбойного сектора на жестком диске, мы не можем послать “запрос на повторную передачу” в прошлое - в то время, когда сектор нормально читался. Все что мы можем сделать - это записать избыточные данные в другой сектор или на другой диск заранее.

Бывает и так, что организация обратной связи осложнена практическими ограничениями. Обратный канал связи может быть слишком дорог и/или слишком медленен. Задержка передачи сигнала с Земли на космический аппарат и обратно может составлять от секунд (орбита Луны) до часов (Вояждеры, Пионеры, Кассини, Новые горизонты, и т.д.) и требует многометровых параболических антенн. Если посчитать пропускную способность TCP/IP для связи с Луной, то получится, что с настройками по-умолчанию (и вне зависимости от реальной ширины канала) скорость передачи данных будет не более 175 Kbps.

Вообще сценариев, когда помехоустойчивое кодирование выгоднее запросов на повторную передачу - масса. Передача данных по радиоканалу, высокоскоростная передача данных, высокочастотная торговля на бирже, синхронизация часов по сети, системы глобального позиционирования и т.д. Во многих из них фонтанный код может быть хорошим выбором.

Алгоритм работы фонтанного кода на удивление прост. Исходное сообщение разбивается на блоки одинакового размера пронумерованные от 1 до k. Каждый исходящий пакет генерируется так:

1. Передатчик выбирает степень связности пакета d в диапазоне от 1 до k.
2. Передатчик выбирает d случайных блоков из исходного сообщения и складывает их по модулю 2 (xor).
3. Результат сложения вместе информацией об исходных блоках посылается приемнику.

Процедура декодирования не намного сложнее. Для каждого входящего пакета выполняются следующие шаги:

1. Пакет помещается в очередь еще не декодированных пакетов вместе со списком исходных блоков.
2. Каждый уже декодированный исходный блок складывается по модулю 2 с пакетом и удаляется из списка.
3. Если в списке исходных блоков остался только один блок, то содержимое пакета и есть исходный блок. Блок помечается как декодированный. Пакет удаляется из очереди.
4. Блок, декодированный на предыдущем шаге, складывается со всеми пакетами из очереди, ссылающимися на него. Это, в свою очередь, может привести к декодированию других пакетов и т.д.

Процесс декодирования легче проследить на конкретном примере. Предположим приемник получил пять однобайтовых пакетов. На рисунке снизу полученные пакеты показаны слева; исходные блоки, которые нужно восстановить, - справа. Четвертый пакет содержит только второй исходный блок, что позволяет сразу его декодировать:

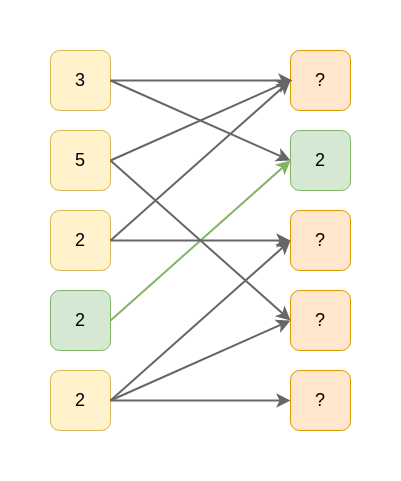
Декодированный исходный блок складывается с первом пакетом по модулю 2 (2^3=1), так как они связаны:

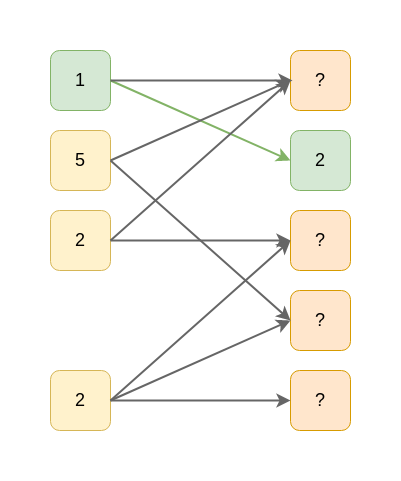
Теперь первый исходный блок может быть также декодирован:

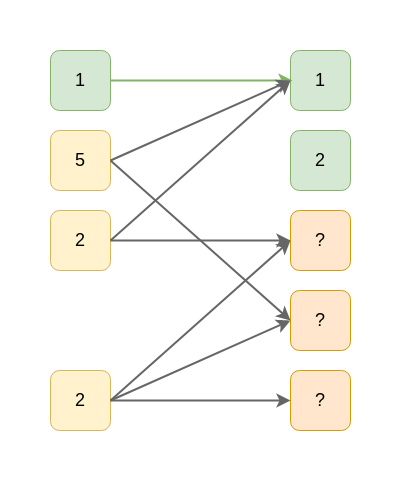
Это, в свою очередь позволяет декодировать исходные блоки 3 и 4 (1^5=4, 1^2=3):

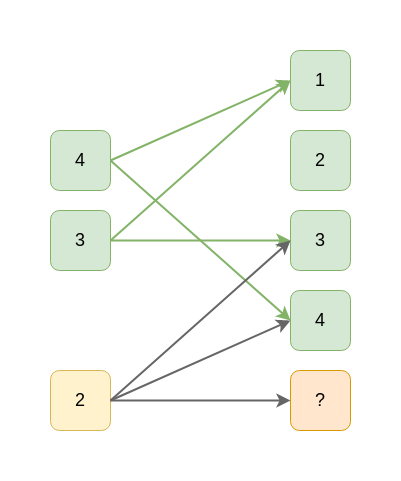
И, наконец, последний исходный блок тоже может быть декодирован:

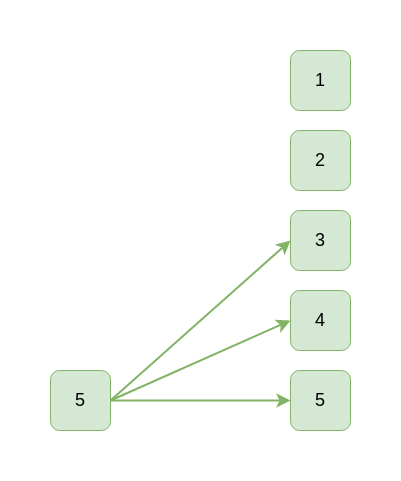
Заметьте, что передатчик и приемник могут передавать и получать пакеты в любом порядке и приемнику совершенно не требуется собрать непрерывную последовательность пакетов. Также, и это не очевидно на первый взгляд, передача информации о связях между пакетами и исходными блоками не требует заметных накладных расходов. Передатчик и приемник могут просто использовать заранее известную псевдослучайную последовательность чисел и передавать номер пакета в этой последовательности.

Я рекомендую прочитать подробный анализ нескольких разновидностей фонтанного кода за авторством Дэвида Макая. Легко заметить, что способность фонтанного кода восстанавливать потерянные пакеты зависит от того, как выбирается степень связности d для каждого пакета. С одной стороны, для того чтобы начать декодирование приемник должен получить хотя бы один пакет со степенью связности 1. С другой стороны, пакеты с большими степенями связности позволяют приемнику восстанавливать данные из потерянных пакетов.

В своей работе Дэвид начинает разбор с простой модели, которая просто генерирует K случайных бит для каждого пакета и добавляет исходный блок i к пакету в случае, если бит с номером i установлен в единицу. Такая модель обладает довольно неплохими способностями к восстановлению потерянных данных, однако она требует значительных вычислительных затрат при больших K (вычислительная сложность алгоритма - O(K^3)).

Далее автор переходит к разбору LT code, который уменьшает количество связей между пакетами и исходными блоками, тем самым снижая вычислительную сложность алгоритма до O(K log K). Эта схема базируется на наблюдении, что в идеальном случае, на каждой итерации у приемника будет только один пакет со степенью связности 1 и декодирование очередного исходного блока будет приводить к появлению очередного пакета со степенью связности 1.

Следующая разновидность фонтанного кода, - Raptor code, улучшает вычислительную сложность до O(K). Иными словами, вычислительная сложность это алгоритма растет от размена исходного сообщения точно также, как растет вычислительная сложность memcpy()! Raptor code использует LT code со средней степенью связности около 3 (вместо log K). Это означает, что приемник увидит много пакетов с малой степенью связности, но некоторые исходные блоки не будут связаны ни с одним пакетом и, соответственно, не смогут быть восстановлены. Raptor code красиво обходит это ограничение с помощью двухступенчатого кодирования: сначала исходные данные кодируются кодом с малой плотностью проверок на чётность (LDPC), а затем слабым LT кодом. Параметры LDPC подбираются так, чтобы он мог восстановить данные, не восстановленные LT кодом. Получается, что Raptor code объединяет способность LDPC гарантированно восстанавливать данные (с определенным уровнем потерь) со способностью LT кода восстанавливать данные при любом уровне потерь.

Raptor code и RaptorQ code стандартизированы Инженерным советом Интернета и способны крайне эффективно восстанавливать данные. Например RaptorQ гарантирует следующую вероятность доставки исходного сообщения:

• Более 0.99 после получения K пакетов
• Более 0.9999 после получения K+1 пакетов
• Более 0.999999 после получения K+2 пакетов

Правами на Raptor code и RaptorQ code обладает Qualcomm, Inc., однако согласно IPR 1957 и IPR 2554 Qualcomm, Inc. обязуется либо выдавать лицензию либо не предъявлять претензий (в зависимости от того, где используется лицензируемый протокол).